algebre

Algèbre des interféromètres ultra-suppresseurs

A partir d'un réseau 1D à la Prouhet, on peut définir des familles d’autres réseaux interférométriques suppresseurs :

réseaux 2D de télescopes identiques

Réseaux 1D et 2D de télescopes de différentes tailles

Réseaux de télescopes où les déphasages ne sont pas forcément π

Réseaux à deux dimensions

Il suffit de considérer deux suites 1D à la Prouhet, : P et Q où les deux symboles a et b sont remplacés par + et - et d'en faire le produit extérieur pour obtenir une matrice de + et de - : R_i,j = P_i x Q_j . On applique alors aux télescopes situés au point i,j le signe de l'élément R_i,j .
La figure suivante illustre la chose en montrant en outre trois exemples dont le premier est une configuration connue sous le nom de croix d'Angel.

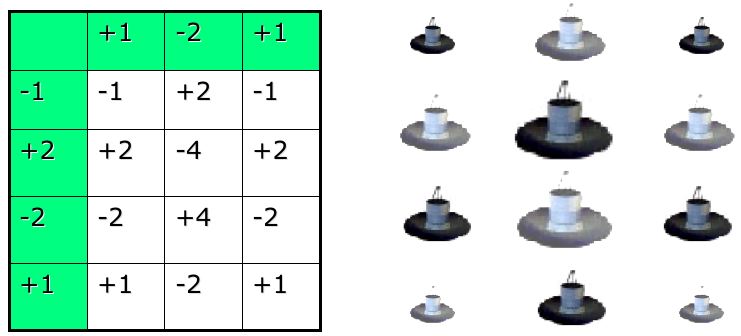
On montre que ces réseaux interférométriques ont bien sûr la propriété d'être des ultra-suppresseurs, mais ce coup-ci dans les deux directions x et y.

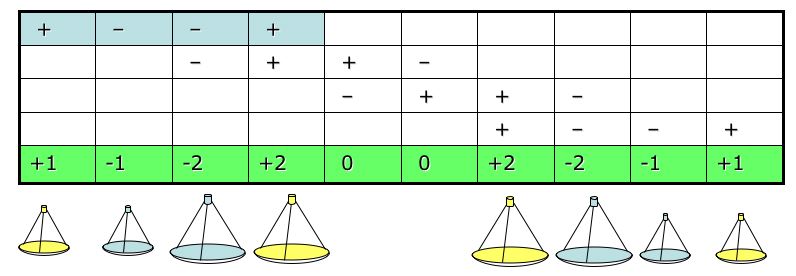
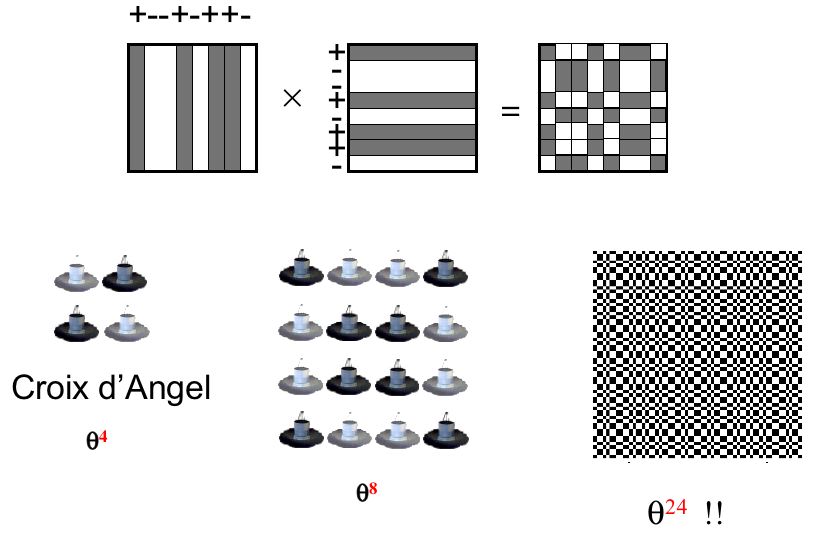
Généralisation des réseaux 1D

On généralise les réseaux à une dimension en appliquant la recette suivante :

On part d'un réseau 2D (voir ci-dessus)

Un cisaillement de n pas est appliqué : c'est à dire que la seconde ligne est décalée de n éléments, la troisième de 2n éléments etc. jusqu'à,la dernière ligne

On réalise la projection suivant X en sommant algébriquement les colonnes, ce qui donne la surface du télescope correspondant et son signe (déphasage de π appliqué ou non)

La figure suivante illustre la recette et son résultat dans le cas d'un réseau de départ 4x4 et d'un cisaillement n=2

Généralisation des réseaux à 2 Dimensions

Un couple de réseaux 1D permet de créer un réseau 2D suivant la même recette du produit extérieur vue plus haut : si P et Q sont des réseaux 1D généralisés, on obtient le réseau généralisé R à 2D dont l'élément est : R_i,j = P_i x Q_j . La figure suivante illustre une telle production d'un réseau 2D ultra-suppresseur :